[머신러닝] 군집화 # 3. GMM (Gaussian Mixture Model)
이 글은 책 「파이썬 머신러닝 완벽가이드」와 공돌이의 수학정리노트 깃허브 글을 바탕으로 작성되었습니다.
GMM(Gaussian Mixture Model)란?
여러 개의 정규분포를 이루는 데이터가 합쳐진 집합(모집단)에서 데이터가 추출된 것(표본)이라는 가정하에 군집화를 수행하는 알고리즘
GMM에서의 모수 추정 : 1. 개별 정규 분포의 평균과 분산 2. 각 데이터가 어떤 정규 분포에 해당하는지의 확률
MLE(Maximum Likelihood Estimation, 최대우도법)이란?
1. MLE 정의
모수적(parametic)인 밀도 추정 방법으로 파라미터 \( \theta = (\theta_{1}, \cdots, \theta_{m}) \) 으로 구성된 어떤 확률 밀도함수 \( P(x| \theta) \) 에서 관측된 표본 데이터 집합을 \( x=(x_{1}, x_{2}, \cdots, x_{n}) \) 이 표본들에서 파라미터 \( \theta = (\theta_{1}, \cdots, \theta_{m}) \)를 추정하는 방법
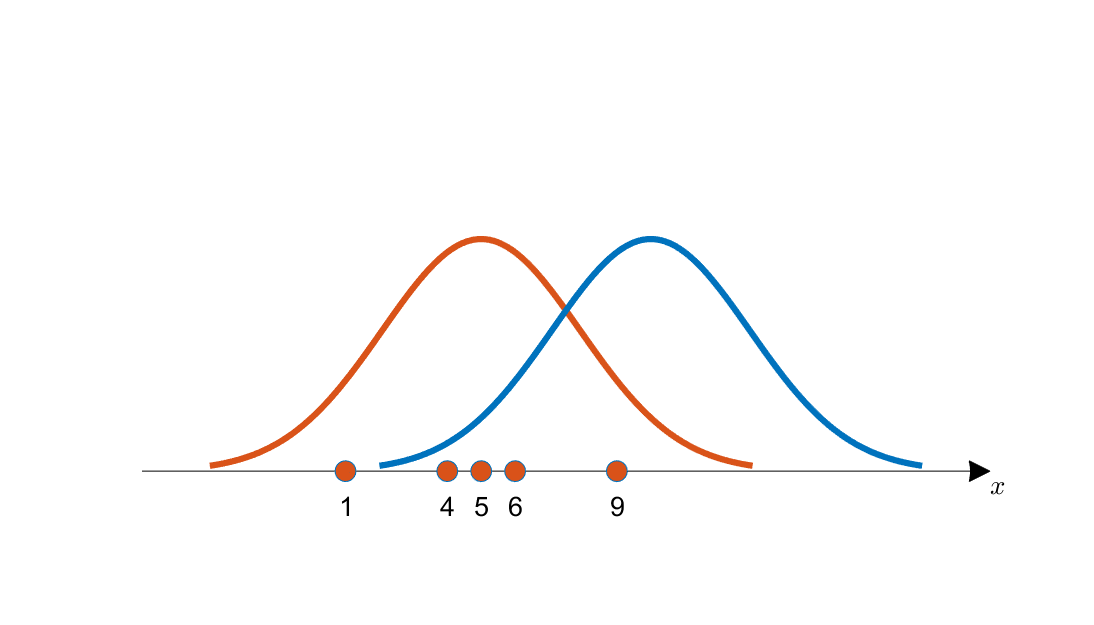
(예) 아래의 그림에서 관측된 데이터는 파란색 곡선보다 주황색 곡선으로부터 추출된 가능성이 더 커보인다. 데이터를 통해서 주황색 곡선의 평균과 분산을 구하는 것이 MLE의 목표이다.
2. 결합 확률 밀도 함수(Likelihood Function)
- 가능도(Likelihood) : 획득한 데이터가 특정 분포로부터 나왔을 가능성을 의미한다. 데이터가 추출되었다고 추정되는 후보 분포에서 함수값(높이)를 말한다.
- 결합 확률 밀도 함수 (Likelihood Function) : 각 데이터 샘플에서 후보 분포에 대한 높이를 모두 곱한 것, 이 함수 값이 커지는 \( \theta \) 를 추정값 \( \hat{\theta} \) 로 본다.
cf. 높이를 더하지 않고 곱하는 이유는 모든 데이터 추출이 독립적으로 일어나는 사건이기 때문이다.
$$P(x|\theta) = \prod_{k=1}^{n}P(x_{k}|\theta)$$
- 로그-결합 확률 밀도 함수 (Log-Likelihood Function)
$$L(\theta|x) = log P(x|\theta) = \sum_{i=1}^{n} log P(x_{i}|\theta) $$
3. 결합 확률 밀도 함수에서 최댓값을 찾는 방법
- 계산의 편의를 위해 로그-결합 확률 밀도 함수를 사용하고 편미분함수=0을 이용한다.
$$ \frac{\delta}{\delta \theta}L(\theta|x) = \frac{\delta}{\delta \theta} log P(x|\theta) = \sum_{i=1}^{n} \frac{\delta}{\delta \theta}log P(x_{i}|\theta) = 0$$
4. 모평균, 모분산 추정
MLE을 통해 증명이 가능하다. 아래의 조건식을 만족할 때 결합 확률 밀도 함수가 최대가 된다.
- 모평균 : $$\hat{\mu} = \frac{1}{n} \sum_{i=1}^{n} x_{i}$$
- 모분산 : $$\hat{\sigma}^{2} = \frac{1}{n} \sum_{i=1}^{n}(x_{i}-\mu)^{2}$$
5. 넘어가기 전에
수직선 상에 데이터가 10개 주어져있고, 각 데이터에 label이 주어져있다고 가정해보자.
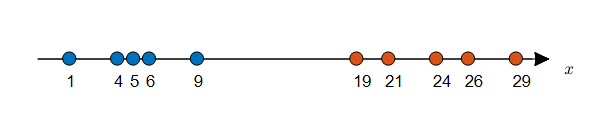
MLE 방식을 통해 각 클래스에 따른 모평균, 모분산 추정을 통해 확률 분포를 알아낼 수 있다.

하지만 label이 주어지지 않는다면? 모평균과 모분산 추정이 불가능하다. → EM 사용
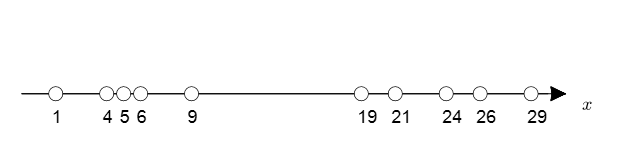
EM(Expectation and Maximization, 기댓값 최대화 알고리즘)이란?
데이터에 label이 주어지지 않을 경우 데이터가 정규 분포를 이루는 데이터 집합(모집단)으로부터 추출되었다고 가정하고 군집화를 수행하는 알고리즘 = GMM(Gaussian Mixture Model)
작동 과정
1. 각 클래스별로 임의의 모수 \( (\mu, \sigma) \) 을 지정하고 각 클래스에 대한 분포를 알아낸다.
2. 각 클래스에 따른 분포가 주어지면, 각 데이터에 대한 분포의 함수값(높이, 가능도, Likelihood)를 비교하여 각 데이터에 라벨링을 해준다.
3. 동일한 라벨링을 한 군집을 묶어 평균과 표준편차를 계산하고, 새로운 분포를 바탕으로 새로운 라벨링을 수행한다.
GMM과 K-평균 비교
사이킷런 클래스 GMM
class sklearn.mixture.GaussianMixture(n_components=1, *, covariance_type='full', tol=0.001, reg_covar=1e-06, max_iter=100, n_init=1, init_params='kmeans', weights_init=None, means_init=None, precisions_init=None, random_state=None, warm_start=False, verbose=0, verbose_interval=10)주요 인자
- n_components : 군집 개수
- max_iter : 최대 반복 횟수
장점
- KMeans보다 다양한 데이터 세트에 유연하게 적용될 수 있음
단점
- 수행시간이 오래 걸림
GMM과 K-평균 비교 (+평균이동)
- 원형 구조의 데이터에는 K-평균이 군집화를 잘 수행
- 길죽한 구조의 데이터 세트에는 K-평균이 군집화를 잘 수행하지 못하고, GMM이 더욱 효과적
- 평균 이동의 경우 최적화된 대역폭에 맞춰서 최적의 군집 개수를 자동으로 계산하는데, 그 결과가 GMM의 군집 결과만큼 효율적이어 보이지는 않는다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans, MeanShift, estimate_bandwidth
from sklearn.mixture import GaussianMixture
# make dataset
X, y = make_blobs(n_samples=300, n_features=2, centers=3, cluster_std=0.5, random_state=0)
tf = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_tf = np.dot(X, tf)
df = pd.DataFrame(X_tf, columns=['ftr1','ftr2'])
df['target'] = y
# KMeans
kmeans = KMeans(n_clusters=3, random_state=0)
df['kmeans_label'] = kmeans.fit_predict(X_tf)
# GMM
gmm = GaussianMixture(n_components=3, random_state=0)
df['gmm_label'] = gmm.fit_predict(X_tf)
# MeanShift
best_h = estimate_bandwidth(X_tf)
meanshift = MeanShift(bandwidth=best_h)
df['meanshift_label'] = meanshift.fit_predict(X_tf)
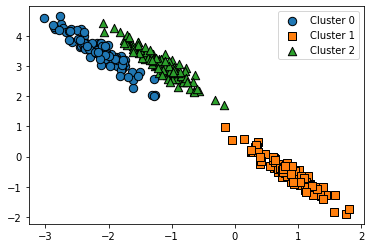
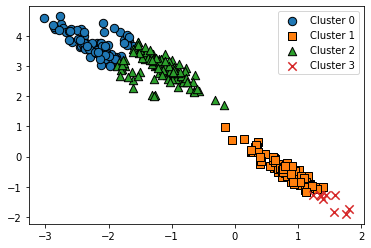
# plot
visualize_cluster_plot(kmeans, df,'kmeans_label', iscenter=True )
visualize_cluster_plot(gmm, df, 'gmm_label', iscenter=False)
visualize_cluster_plot(meanshift, df, 'meanshift_label', iscenter=False)


참고 문헌
- 권철민, 「파이썬 머신러닝 완벽가이드」, 위키북스, 2020, p.409~465
- 공돌이의 수학정리노트, "최대우도법(MLE)", https://angeloyeo.github.io/2020/07/17/MLE.html
- 공돌이의 수학정리노트, "GMM과 EM알고리즘", https://angeloyeo.github.io/2021/02/08/GMM_and_EM.html